用实用的python示例来掌握K-Nearest邻居（K-NN）（示例.邻居.实用.NN.python...）

wufei1232025-02-15python12

k-近邻算法(k-nn)详解及python实现

想象一下，您初来乍到一个新城市，想找一家不错的餐厅。您不熟悉当地情况，于是向三位当地人征求意见。

• 两位推荐餐厅A。 • 一位推荐餐厅B。

由于大多数人推荐餐厅A，您决定去那里用餐。

这个简单的决策过程，正是机器学习中K-近邻(K-NN)算法的工作原理！本文将深入探讨K-NN算法，了解其机制，并通过一个Python实例进行演示。

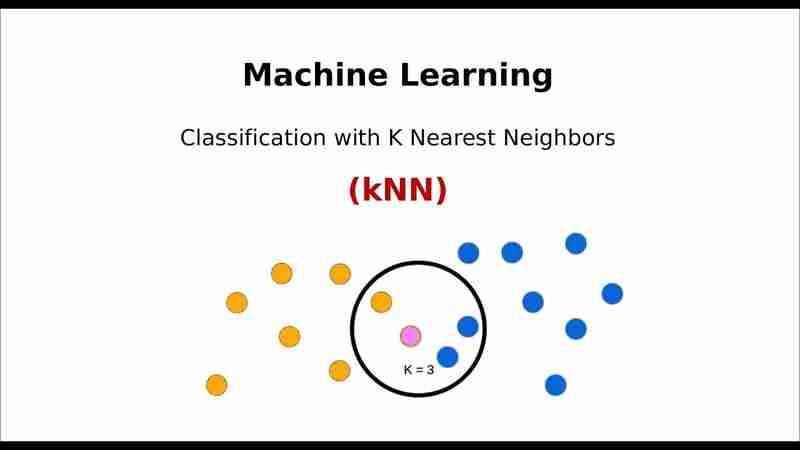
用实用的python示例来掌握K-Nearest邻居（K-NN）

什么是K-近邻算法(K-NN)?

K-NN算法是一种监督学习算法，用于分类和回归。它基于这样一个假设：相似的样本更可能属于同一类别。算法通过计算新数据点与现有数据点之间的距离，找到与其最近的K个邻居，并根据这些邻居的类别来预测新数据点的类别。

K-NN算法工作流程：

选择邻居数量(K)：这是一个超参数，需要根据数据集进行调整。
计算距离：计算新数据点与数据集所有其他数据点之间的距离（常用欧几里得距离或曼哈顿距离）。
选择K个最近邻：选择距离新数据点最近的K个数据点。
多数投票：根据这K个最近邻的类别，通过多数投票确定新数据点的类别（对于分类问题）。对于回归问题，则取K个最近邻的平均值作为预测结果。

Python实现K-NN

我们将使用一个数据集来预测一个人是否会根据年龄和预计收入购买产品。

步骤1：导入必要的库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

步骤2：创建示例数据集

data = {
    'age': [22, 25, 47, 52, 46, 56, 55, 60, 62, 61, 18, 24, 33, 40, 35],
    'estimatedsalary': [15000, 29000, 43000, 76000, 50000, 83000, 78000, 97000, 104000, 98000, 12000, 27000, 37000, 58000, 41000],
    'purchased': [0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0]  # 1: purchased, 0: not purchased
}
df = pd.DataFrame(data)
print(df.head())

步骤3：数据预处理

x = df[['age', 'estimatedsalary']]
y = df['purchased']

# 分割训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)

# 特征缩放(标准化)
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

步骤4：训练K-NN模型

k = 3
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(x_train, y_train)

步骤5：预测和模型评估

y_pred = knn.predict(x_test)

# 评估性能
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
report = classification_report(y_test, y_pred)

print(f"Accuracy: {accuracy:.2f}")
print("Confusion Matrix:
", conf_matrix)
print("Classification Report:
", report)

关键洞察：